
How I learned hexadecimal?
X-Com
TL;DR: No Google, no Stack Overflow, no Wikipedia at that time (1994). I learned hexadecimal with the game X-COM: UFO Defense.

UFO: Enemy Unknown (X-COM: UFO Defense in North America) is a strategy video game and it was released in March 1994 for MS-DOS. [Source]
Here is the trailer:
X-Com UFO Enemy Unknown Intro 1994
What is the link between this masterpiece game and the hexadecimal?
Well this is with this game that I learned the hexadecimal (and more).
How?
By cheating !!!
99999999
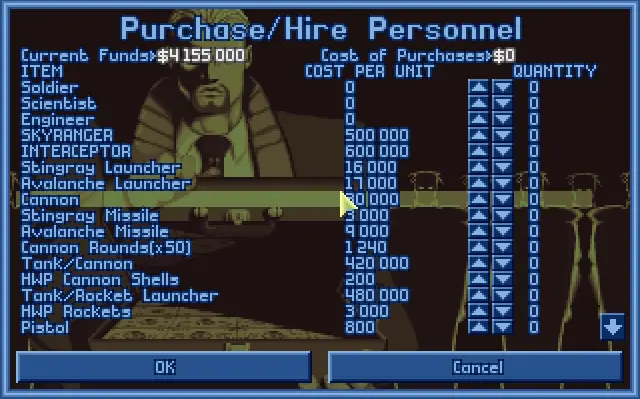
Here is the base menu inside XCOM and there is a "Purchase/Recruit" button (bottom-right).
If we click on this button, the purchase menu appears and we can buy or sell items:
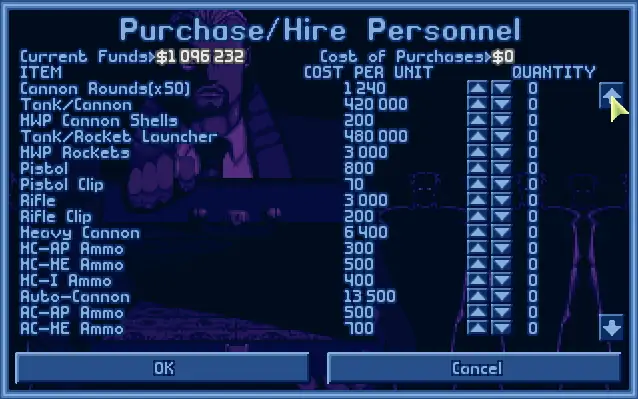
I saved the game in the first slot and inside the XCOM folders structure,
there is a folder called "GAME_1":
**GAME_1**, GAME_10, GAME_2, GAME_3, GAME_4, GAME_5,
GAME_6, GAME_7, GAME_8, GAME_9, GEODATA, GEOGRAPH, MAPS,
MISSDAT, ROUTES, RUNEXE, SOUND, TERRAIN, UFO2EXE,
UFOEXE, UFOGRAPH, UFOINTRO, UNITS
All files inside the "GAME_1" folder:
ACTS.DAT, AKNOW.DAT, ALIEN.DAT, ASTORE.DAT, BASE.DAT, BGLOB.DAT, BPROD.DAT,
CRAFT.DAT, DIPLOM.DAT, DUM.BIN, FACIL.DAT, GEODATA.DAT, IGLOB.DAT, INTER.DAT,
LEASE.DAT, LIGLOB.DAT, LOC.DAT, MAP.DAT, MISDATA.DAT, MISSIONS.DAT, OBPOS.DAT,
PRODUCT.DAT, PROJECT.DAT, **PURCHASE.DAT**, RESEARCH.DAT, ROUTES.DAT, SAVEINFO.DAT,
SEEMAP.DAT, SMOKBIT.DAT, SMOKREF.DAT, SOLDIER.DAT, SOURCEMP.DAT, TERMP.DAT, TRANSFER.DAT, UIGLOB.DAT, UNITPOS.DAT, UNITREF.DAT, UP.DAT, WGLOB.DAT,XBASES.DAT, XCOM.DAT, ZONAL.DAT,
There is a file named "PURCHASE.DAT" which is the same name that the purchase menu above.
So I decided to use the "debug.com" executable to edit this file.
"The line-oriented debugger DEBUG is an external command in operating systems such as DOS, OS/2 and Windows.
DEBUG can act as an assembler, disassembler, or hex dump program allowing users to interactively examine memory contents (in assembly language, hexadecimal or ASCII), make changes, and selectively execute COM, EXE and other file types. It also has several subcommands which are used to access specific disk sectors, I/O ports and memory addresses."
[Source]
Here is the first 128 bytes of "PURCHASE.DAT" file:
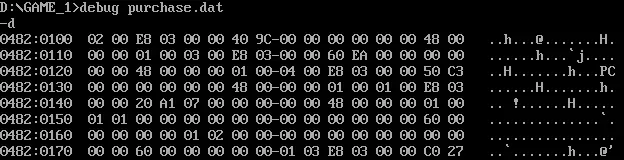
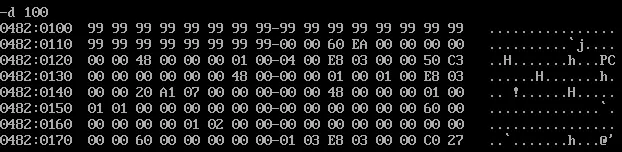
At that time (1994), I didn't know what was the maximal digit in hexadecimal and I tough 9 was the maximal digit so I entered a lot of 9 to overwrite memory:

"PURCHASE.DAT" file with a lot of 99999999:
Here is the result when I relaunched the game and loaded my save game:
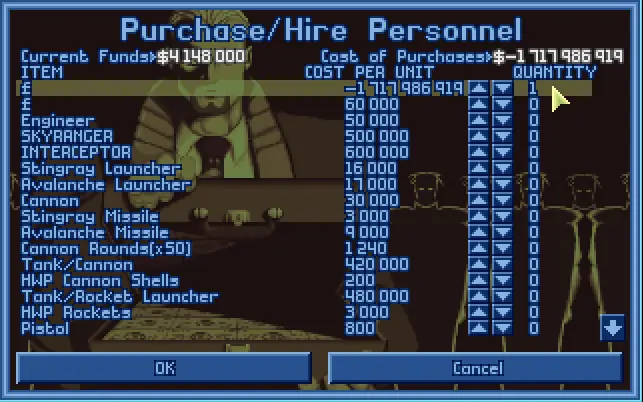
The first item looks like the Pound sterling which cost -1717986919 and I'm able to buy this item since -1717986919 <= 4148000. I think the pseudo code could be like that:
if (itemCost <= currentFunds)
{
currentFunds = currentFunds - itemCost;
// currentFunds = 4148000 - -1717986919; // 2 negatives make a positive
// 1722134919 = 4148000 + 1717986919;
}
else
{
print("NOT ENOUGH MONEY!");
}
I duplicated the "PURCHASE.DAT" file before to edit so I can restore after the "cheat".
Now I have plenty of cash... but I like to play without cheating.
How I was able to use debug.com?
I like/liked to experiment and I launched all commands and executables I was able to find at that time in DOS. I also deleted 3 times my root folder (command.com included) the first month I got my first computer ... After that, I learned this useful command "attrib +r +h +s".
I was also reading an assembly language book and I got some tips from this book (e.g. how to display a message in assembly with debug.com).
Binary
Before seeing the hexadecimal, let's visit the binary first.
A binary number is a number expressed in the base-2 (bit), which uses only two symbols: typically "0" (zero/false) and "1" (one/true).
Bit /
Binary number
1 bit: 0 or 1 (2 possibilities, 2^1)
1 byte = 8 bits (256 possibilities, 2^8)
2 bytes = 16 bits (65536 possibilities, 2^16)
4 bytes = 32 bits (4294967296 possibilities, 2^32)
8 bytes = 64 bits (18446744073709551616 possibilities, 2^64)
1 Nibble / Half Byte = 4 bits (16 possibilities, 2^4)
The way I learned to convert decimal to binary in school (1999-2000) was by division, remainder and reverse order. I didn't like this solution and I like more my version which is to create a table from the right to left by doubling the number (starting with 1) every time like that:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
Now let's take a random value: 81 (decimal value).
Based on the table above, we need to look for the closest value equal or less than 81 which is 64.
We add 1 inside the case 64:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 |
We subtract 64 like that: 81-64 = 17.
We apply the same pattern (less or equal) for 17 which is 16.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1 |
17-16 = 1;
Same thing for 1
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 |
Now, we fill the remaining empty cases with 0
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
81 in binary is 01010001.
If we want to convert from binary to decimal, it's pretty easy. We just need to sum cases that are flagged "1" : (64 + 16 + 1) = 81;
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
Another example below (128 + 4 + 2 +1) = 135 = 10000111;
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Hexadecimal
Now we will convert decimal or binary in hexadecimal.
Binary is in base-2 [0..1]
Decimal is in base-10 [0..9]
Hexadecimal is in base-16 where the high digits are letters like ABCDEF [0123456789ABCDEF].
| Decimal | Hexadecimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Hexadecimal is like a Nibble/Half Byte where it regroups 4 bits together (four-bit aggregation).
So one byte (8 bits) is represented by two hexadecimal digits (e.g. A0, FF, 10, 99).
Now, let's use the two previous examples (81 and 135) and convert in hexadecimal.
We will add 2 news rows to help for the conversion.
The third row regroups 4 columns (8,4,2,1) which represents 4 bits (a digit in hexadecimal).
The fourth row represents the sum and value in hexadecimal.
(64 + 16 + 1) = 81 (in decimal) = 01010001 (in binary) = 51 (in hexadecimal)
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 5 (4 + 1) | 1 | ||||||
(128 + 4 + 2 +1) = 135 (in decimal) = 10000111 (in binary) = 87 (in hexadecimal);
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 8 | 7 (4 + 2 + 1) | ||||||
(128 + 64 + 32 + 16 + 8 + 4 + 2) = 254 (in decimal) = 11111110 (in binary) = FE (in hexadecimal);
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| F (8 + 4 + 2 + 1) | E (8 + 4 + 2) | ||||||
Hexadecimal numbers are usually written with "0x" before the number to avoid confusion with decimal: 0x51, 0x87, 0xFE, 0x9999, 0xFFFFFFFF, ...
[Tip of the post]
You can use the Windows Calculator for conversion between binary, hexadecimal and decimal.
You need to change the "Standard" view to "Programmer" view.
Microsoft released the code source of this calculator on GitHub a couple of months ago.
Signed versus Unsigned

Now we know how to convert in hexadecimal and binary but we didn't figure out why a lot of 99999999 display -1717986919 ???
Here is the table conversion between hexadecimal and decimal with 99, 9999, ...
| # | Hexadecimal | Decimal |
|---|---|---|
| 1 byte | 0x99 | 153 |
| 2 bytes | 0x9999 | 39321 |
| 3 bytes | 0x999999 | 10066329 |
| 4 bytes | 0x99999999 | 2576980377 |
No -1717986919 there...
In computer/programming, the same data value (1 byte, 2 bytes, ...) will display differently depending if we use in signed or unsigned mode.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| F (8 + 4 + 2 + 1) | F (8 + 4 + 2 + 1) | ||||||
(128 + 64 + 32 + 16 + 8 + 4 + 2 + 1) = 0xFF = 255 in unsigned mode and -1 in signed mode.
[C# example code]
byte unsignedByte = 0xFF;
sbyte signedByte = (sbyte)unsignedByte;
print("unsigned:" + unsignedByte + " signedByte:" + signedByte); // unsigned:255 signedByte:-1
// "byte" stands for unsigned byte. "sbyte" stands for signed byte. Both take 8 bits space in the memory.
// Output: unsigned:255 signedByte:-1
Below is the reference between unsigned/signed on 1-2-4 bytes format:
[1 bit]
- 2 possibilities, 2^1
- range [0..1]
[1 byte]
- 8 bits (256 possibilities, 2^8)
- range for unsigned [0..255]
- range for signed [-128..127]
[2 bytes]
- 16 bits (65536 possibilities, 2^16)
- range for unsigned: [0..65535]
- range for signed: [-32768..32767]
[4 bytes]
- 32 bits (4294967296 possibilities, 2^32)
- range for unsigned: [0..4294967295]
- range for signed: [-2147483648..2147483647]
if we are in "signed" mode, the highest bit (128 for this case, 1 byte) will determine if the number is signed (1) or unsigned (0)
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| F (8 + 4 + 2 + 1) | F (8 + 4 + 2 + 1) | ||||||
"In computing, the most significant bit (MSB, also called the high-order bit) is the bit position in a binary number having the greatest value. The MSB is sometimes referred to as the high-order bit or left-most bit due to the convention in positional notation of writing more significant digits further to the left.
The MSB can also correspond to the sign bit of a signed binary number. In one's and two's complement notation, "1" signifies a negative number and "0" signifies a positive number."
[Source]
1 byte "signed" mode
11111111 = -1;
00000001 = 1;
2 bytes "signed" mode
11111111 11111111 = -1;
00000000 00000001 = 1;
4 bytes "signed" mode
11111111 11111111 11111111 11111111 = -1;
00000000 00000000 00000000 00000001 = 1;
1 byte "unsigned" mode
11111111 = 255;
00000001 = 1;
2 bytes "unsigned" mode
11111111 11111111 = 65535;
00000000 00000001 = 1;
4 bytes "unsigned" mode
11111111 11111111 11111111 11111111 = 4294967295;
00000000 00000000 00000000 00000001 = 1;
How to convert a positive number to a negative number?
Two's complement
"To get the two's complement of a negative binary number, the bits are inverted, or "flipped", by using the bitwise NOT operation; the value of 1 is then added to the resulting value, ignoring the overflow which occurs when taking the two's complement of 0.
For example, using 1 byte (=8 bits), the decimal number 5 is represented by
0000 0101
The most significant bit is 0, so the pattern represents a non-negative value. To convert to −5 in two's-complement notation, first, the bits are inverted, that is: 0 becomes 1 and 1 becomes 0:
1111 1010
At this point, the representation is the ones' complement of the decimal value 5. To obtain the two's complement, 1 is added to the result, giving:
1111 1011
The result is a signed binary number representing the decimal value −5 in two's-complement form. The most significant bit is 1, so the value represented is negative.
The two's complement of a negative number is the corresponding positive value, except in one special case. For example, inverting the bits of −5 (above) gives:
0000 0100
And adding one gives the final value:
0000 0101
Likewise, the two's complement of zero is zero: inverting gives all ones, and adding one changes the ones back to zeros (since the overflow is ignored).
"
[Source]

Let's try the two's complement on this number: 1717986919
1717986919 is 01100110 01100110 01100110 01100111 in binary.
Flip/Invert bits: 10011001 10011001 10011001 10011000.
Add the value 1: 10011001 10011001 10011001 10011001.
The four bytes look similar so let's convert only one byte.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 9 (8 + 1) | 9 (8 + 1) | ||||||
0x99 in hexadecimal
The "COST PER UNIT" inside the "PURCHASE.DAT" works in 4 signed bytes.
0x99999999 = -1717986919
Free Resources
Now that we know how hexadecimal works, let's analyse some items and change those values.
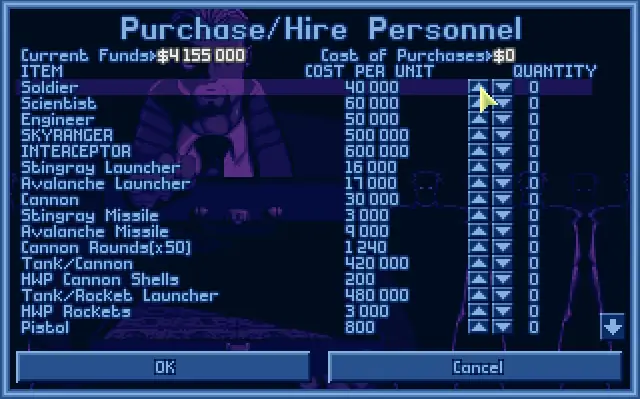
- A Soldier costs 40000 (in decimal), 0x9C40 (in hexadecimal)
| 32768 | 16384 | 8192 | 4096 | 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 9 (8+1) | C (8+4 = 12) | 4 | 0 | ||||||||||||
- A Scientist costs 60000 (in decimal) and it's 0xEA60 (in hexadecimal)
| 32768 | 16384 | 8192 | 4096 | 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| E (8+4+2 = 14) | A (8+2 = 10) | 6 (4+2) | 0 | ||||||||||||
- An Engineer costs 50000 (in decimal), 0xC350 (in hexadecimal)
| 32768 | 16384 | 8192 | 4096 | 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| C (8+4 = 12) | 3 (2+1) | 5 (4+1) | 0 | ||||||||||||
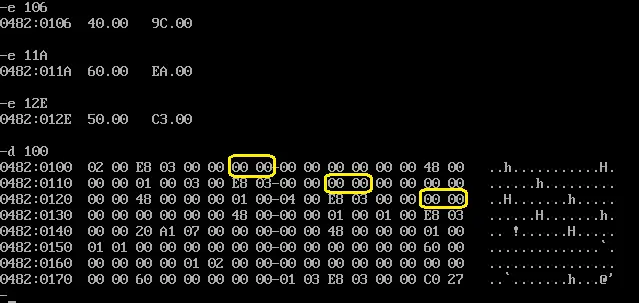
Let's open "PURCHASE.DAT" file again (the original version) and we need to find those
value:
0x9C40 -> 40 9C
0xEA60 -> 60 EA
0xC350 -> 50 C3
Why inverse? (e.g. 0xABCD -> CD AB), look for Endianness / Little-Endian.

I replaced those values with 0.
After the modification, we can get free resources as soldier, scientist and engineer.
Checksum

At that time I didn't know about the "checksum" mechanism but later I learned about that.
I'm still try to understand why they didn't add any checksum inside the save game to see if it is corrupted or tampered. Maybe a short deadline?
Some interesting checksums:
Reddit: Starcraft used a simple 13-digit CD key algorithm that was easy to bypass. The 13th digit verified the first 12. You could enter anything for the first 12 digits, and guess the 13th (there's only 10 possibilities), leading to the infamous 1234-56789-1234
[Source]
For old-school CD keys, it was just a matter of making up an algorithm for which CD keys (which could be any string) are easy to generate and easy to verify, but the ratio of valid-CD-keys to invalid-CD-keys is so small that randomly guessing CD keys is unlikely to get you a valid one.
Starcraft and Half-life both used the same checksum, where the 13th digit verified the first 12. Thus, you could enter anything for the first 12 digits, and guess the 13th (there's only 10 possibilities), leading to the infamous 1234-56789-1234
The algorithm for verifying is public, and looks something like this:
x = 3;
for(int i = 0; i < 12; i++)
{
x += (2 * x) ^ digit[i];
}
lastDigit = x % 10;
Micro versus Macro

If you like more micro management with inventory detail: missile, clip, rockets, ammo... You should play the first X-COM: UFO Defense.
Example: if your "Interceptor" doesn't have any missile, you will not be able to fire missiles.
Same thing if your crew doesn't have any ammo. There is also a second XCOM game in DOS called "X-COM: Terror from the Deep" where some weapons cannot be used on surface/land missions versus underwater... so if you equip your troopers with only underwater weapons and you try a surface/land mission, you will be screwed!!
The recent XCOM (XCOM: Enemy Unknown and XCOM 2) games are more in macro management with better graphics / music / sounds
X-COM: UFO Defense, XCOM: Enemy Unknown and XCOM 2 are excellent. If you are looking for a game to play, you should try!!!
I think I will restart a XCOM campaign!
Thanks for reading,
JS.
